SOLUCIÓN DE ECUACIONES
METODO DE GAUSS JORDAN:
El Método de Gauss – Jordan o también llamado eliminación de Gauss – Jordan, es un método por el cual pueden resolverse sistemas de ecuaciones lineales con n números de variable, encontrar matrices y matrices inversas, en este caso desarrollaremos la primera aplicación mencionada.
Para resolver sistemas de ecuaciones lineales aplicando este método, se debe en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales en su notación matricial.
PASOS:
- De la ecuación tome los valores y arme la matriz ampliada.
- Convierta a 0 la columna 1 las filas 2-3 multiplicando y sumandolas con la fila 1
- Convierta 0 la columna 2 y fila 3 sumandolas y multiplicandolas.
- Divida la fila 3 por el valor de la columna 3 fila 3.
- Convierta 0 la columna 3 fila 1-2.
- Sumando y multiplicando con la fila 3, divido la fila 2 entre el valor de la columna 2, fila 2.
- Convierta 0 la fila 1 columnado, sumando y multiplicando por la fila 2.
- Divida la fila 1 ente el valor de la fila 1 casilla 1.







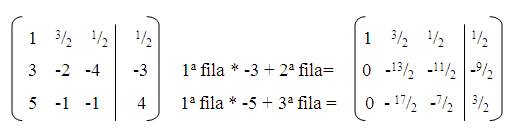
Arreglo de filas y columnas. - Esto se refiere a como se deben de acomodar los datos dentro de una matriz, y la posición que ocupa.
Matriz unidad.
- Esta matriz se refiere a aquella que posee una diagonal con unos, y todos los demás datos son ceros
Orden de una matriz.-
Esto es como se debe de mencionar a las matrices, esto es primero los renglones, luego por, y por último la cantidad de columnas.
Matriz cuadrada.- Esta es aquella matriz la cual tiene igual número de columnas como de renglones.
Matriz colunma.- Es aquella en la que el valor de J = 1.
Matriz renglón.- Es en la que i = 1
Matriz diagonal .- Es aquella en la solo existen valores en j=i
Matriz nula.- Es aquella que para todo aiJ el valor es cero.
- Esta matriz se refiere a aquella que posee una diagonal con unos, y todos los demás datos son ceros
Orden de una matriz.-
Esto es como se debe de mencionar a las matrices, esto es primero los renglones, luego por, y por último la cantidad de columnas.
Matriz cuadrada.- Esta es aquella matriz la cual tiene igual número de columnas como de renglones.
Matriz colunma.- Es aquella en la que el valor de J = 1.
Matriz renglón.- Es en la que i = 1
Matriz diagonal .- Es aquella en la solo existen valores en j=i
Matriz nula.- Es aquella que para todo aiJ el valor es cero.
Matriz simetrica.- Es aquella en la que aiJ = aJi.
DETERMINANTE DE UNA MATRIZ
Metodo de diagonales
Suma de los productos de las diagonales hacia abajo, menos la suma de las diagonales hacia arriba
Metodo de cofactores.- El cofactor de un termino aiJ es el determinante formado por lo que queda de la matriz al anular el renglón i, y la columna j.
El resultado de la matriz es la suma de los cofactores de una columna o renglón.
Matriz singular.- Cuando el determinante de una matriz es igual a cero se dice que es singular.
Matriz transpuesta.- Es intercambiar filas por columnas.
Matriz adjunta.- Es la matriz de cofactores transpuesta
ALGEBRA DE MATRICES*-Adicion ( deben de ser de orden igual, y se realiza de elemento a elemento)
Multiplicación
DETERMINANTE DE UNA MATRIZ
Metodo de diagonales
Suma de los productos de las diagonales hacia abajo, menos la suma de las diagonales hacia arriba
Metodo de cofactores.- El cofactor de un termino aiJ es el determinante formado por lo que queda de la matriz al anular el renglón i, y la columna j.
El resultado de la matriz es la suma de los cofactores de una columna o renglón.
Matriz singular.- Cuando el determinante de una matriz es igual a cero se dice que es singular.
Matriz transpuesta.- Es intercambiar filas por columnas.
Matriz adjunta.- Es la matriz de cofactores transpuesta
ALGEBRA DE MATRICES*-Adicion ( deben de ser de orden igual, y se realiza de elemento a elemento)
Multiplicación
conformabilidad
La matriz resultante de la multiplicación es de orden (n1,m2)
Deben ser iguales para que sean conformables, si no es conformable, no se puede realizar la multiplicación entre la matrices.--Operación (usando la dos matrices anteriores) Primero se revisa que sean conformables.
La multiplicación /A * /B se realiza renglón de la primera matriz por la columna de la segunda.
Para el termino 1,1 de la matriz resultante se mutiplica el renglón 1 por la columna 1
(2)(9)+(-3)(-1)+(4)(5)=41 Este es el termino resultante de la matriz final
Para obtener el termino i, j se multiplica de la manera que ya se vio el renglón i por la columna j.
El resultado de /A * /B es
La matriz resultante de la multiplicación es de orden (n1,m2)
Deben ser iguales para que sean conformables, si no es conformable, no se puede realizar la multiplicación entre la matrices.--Operación (usando la dos matrices anteriores) Primero se revisa que sean conformables.
La multiplicación /A * /B se realiza renglón de la primera matriz por la columna de la segunda.
Para el termino 1,1 de la matriz resultante se mutiplica el renglón 1 por la columna 1
(2)(9)+(-3)(-1)+(4)(5)=41 Este es el termino resultante de la matriz final
Para obtener el termino i, j se multiplica de la manera que ya se vio el renglón i por la columna j.
El resultado de /A * /B es
La multiplicación no es conmutable, es decir que no es lo mismo multiplicar /A * /B que /B * /A.
División
*- Propiedades de la inversa
1) /A es cuadrada
2) /A no debe ser singular
3) si /A-1 existe
4) - /A * /A-1 =1
5) - (/A-1)-1 = /A
6) - (/A * /B)-1 =/B-1 * /A-1
*- Propiedades de la inversa
1) /A es cuadrada
2) /A no debe ser singular
3) si /A-1 existe
4) - /A * /A-1 =1
5) - (/A-1)-1 = /A
6) - (/A * /B)-1 =/B-1 * /A-1
ENTIDADES TRIGONOMETRICAS:
Es una igualdad que asocian entidades trigonométricas, para su demostración se toma el lado derecho y por medio de sustituciones y operaciones matemáticas se llega al valor del otro lado.
1
Relación seno coseno
cos² α + sen²
α = 1
2
Relación secante tangente
sec² α = 1 +
tg² α
3
Relación
cosecante cotangente
cosec² α = 1 +
cotg² α
SOLUCIÓN DE ECUACIONES:
http://es.calameo.com/read/005111454c79ec7c98583
CUENTO: ACELERANDO A TOPE (este es mejor)
Caracteres totales:
(sin espacios): 11.339
(con espacios): 13.763
Paginas:
7
Párrafos:
17
Lineas:
43
Link:
https://es.calameo.com/read/00511145431ee4b6b5c5e
Segundo Cuento:
Link:
http://es.calameo.com/read/0051114549f0ba2297a11
VIDEO.
link:
https://www.youtube.com/watch?v=xVNOxBLygac

